| Indice del artículo |
|---|
| Articulos recomendables para leer. |
| TCordobes |
| Noticia Periodico erronea |
| Iteraciones Sucesiones |
| Todas las páginas |
π, un número normal ¿o no?
- Matemáticas para pensar
- 3 MIN
El número π es una de las constantes matemáticas más importantes que existen, pero además es un número fascinante que goza de una gran popularidad entre el público, tanto el matemático, como el no matemático. No en vano tiene dos celebraciones internacionales en su honor, el “Día de pi” (14 de marzo, 3-14 en inglés) y el “Día de aproximación de pi” (22 de julio, en referencia a la aproximación dada por Arquímedes, 22/7 = 3,1428…).
La relación entre la longitud de una circunferencia y su diámetro, que es como se define el número π, tiene unos 4.000 años de antigüedad. Sin embargo, hasta el año 1.761 no se consiguió demostrar, por el matemático francés Johann H. Lambert (1728-1777), que este es un número irracional. Lo cual significa que π no se puede expresar como el cociente entre dos números enteros, o equivalentemente, si consideramos su expresión decimal, esta tiene infinitos decimales y no es periódica, es decir, no existe un número finito de decimales –conocido como período– que, a partir de un decimal dado, se repita de forma infinita, contrariamente a lo que ocurre con números como 146/825, que es racional y cuya expresión decimal es 0,17696969…, siendo su período 69.
De hecho, la búsqueda de los decimales del número π es una investigación activa hoy en día. Se trata de conocer todos los decimales posibles de π (recordemos que todos es imposible, son infinitos y no hay un patrón finito que se repita). El record de decimales en la actualidad es de … 22.459.157.718.361 dígitos … obtenido por Peter Trueb en 2016.
Por otra parte, podemos preguntarnos, entre los decimales del número π, que son infinitos y sin un patrón finito que se repita, cuáles de las diez cifras básicas 0, 1, 2, …, 9 aparece con más frecuencia, y cuales, con menos, dentro de la expresión decimal del número π, o si por el contrario todas las cifras aparecen en la misma proporción. Si miramos a los 100 primeros decimales del número π,
3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679…
observaremos que las diez cifras básicas, del 0 al 9, aparecen en la siguiente proporción: 8, 8, 12, 11, 10, 8, 9, 8, 12, 14. Si las diez cifras básicas aparecieran en la misma proporción, tendrían que aparecer diez veces cada cifra básica en los 100 primeros números, aunque la verdad es que 100 decimales no son muchos, y necesitaríamos ver más decimales. Por tanto, ¿qué ocurre para 1.000, 10.000, 100.000, o más, decimales?
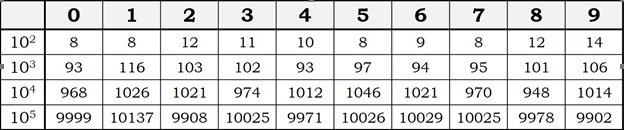
Como podemos observar en la tabla anterior, según va aumentando el número de decimales, la proporción de cada una de las diez cifras básicas dentro de los decimales del número π se van acercando al 10% de los decimales.
En el artículo Digit Statistics of the First 22.4 Trillion Decimal Digits of Pi, su autor, Peter Trueb, nos confirma este hecho entre los 22.459.157.718.361 decimales que se han calculado de la constante geométrica. Más aún, si se toman las 100 secuencias de dos dígitos formadas por las diez cifras básicas, del 00 al 99, cada una aparece en una proporción que se va acercando cada vez más a 1/100, es decir, un 1%. Y lo mismo ocurre para las 1.000 secuencias de tres dígitos, de 000 a 999, cada una de las cuales aparece en una proporción que se va aproximando a 1/1.000. Todas las secuencias posibles son igualmente probables.
Todo esto lo que nos está diciendo es que aparentemente el número π podría ser lo que se conoce como un “número normal” (para la base 10), y que fue introducido por el matemático francés Émile Borel (1871-1956), en 1909. Sin embargo, a día de hoy demostrar la normalidad de π sigue siendo un problema abierto. La supuesta normalidad del número π es lo que nos permite afirmar que dada una secuencia finita de dígitos, como nuestro NIF o número de móvil, llegará un momento entre los decimales de pi en que aparecerá. En internet existen páginas para buscar “tus” números en pi, por ejemplo, subidiom.
La artista donostiarra Esther Ferrer nos acerca a la propiedad de normalidad de π, mediante un contundente argumento visual en el cual asigna un color a cada cifra básica, en su excelente obra Pi (2009-2010). Inspirado por su trabajo os traigo aquí los 399 (más el 3 inicial) decimales del número π, asignando un color distinto a cada una de las cifras básicas.

El triángulo cordobés
- 12 noviembre, 2019
- Matemáticas para pensar
- Por Equipo de edición de Matemáticas de SM
- 3 MIN
Por Ana Casado, editora del equipo de Matemáticas de SM.
En el currículo de Secundaria de Andalucía aparece como contenido “el triángulo cordobés”. Pero…, ¿qué es un triángulo cordobés?
Un triángulo cordobés es un triángulo isósceles cuyos lados están en proporción cordobesa.
El concepto de proporción cordobesa “surge por casualidad, como feliz resultado de un esplendoroso fracaso” como lo explicaba el arquitecto cordobés Rafael de la Hoz Arderiu,s que descubrió y bautizó así a la proporción numérica 1,3.
El arquitecto, amante de las matemáticas, inició un proyecto para certificar la proporción áurea* como canon de belleza universal. Su hipótesis era que a lo largo de historia se había utilizado de forma consciente o inconsciente dicha proporción. Eligió Córdoba para llevar a cabo el estudio por ser una ciudad milenaria donde se habían instalado diversas culturas y por ser su ciudad natal. El resultado fue un fracaso y cancelaron el proyecto. Exceptuando algunos casos puntuales de obras diseñadas por arquitectos no cordobeses, no se encontró la ansiada proporción áurea.

Al poco tiempo, la Diputación de Córdoba le pidió preparar un test de aptitud para asignar becas a estudiantes de Arquitectura. Entre las preguntas propuestas, estaba esta:
“Entre los dos rectángulos siguientes, uno notablemente rechoncho y otro acusadamente alargado (…) tiene que existir un rectángulo equilibrado, bello, perfecto. Dibújenlo”.
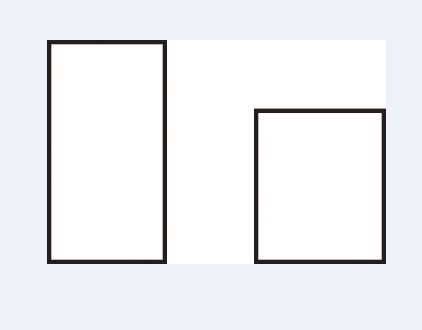
La calificación máxima a esta pregunta se otorgaba al dibujar el rectángulo áureo. El resultado fue sorprendente porque ningún estudiante dibujó el rectángulo áureo, y una mayoría significativa sí dibujó un rectángulo menos esbelto que cumplía la siguiente proporción:
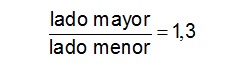
A partir de este resultado, se comenzó una investigación repitiendo esta pregunta a personas residentes o nacidas en Córdoba. La frecuencia de la proporción 1,3 fue igualmente muy alta. ¿Por qué la preferencia por la proporción cordobesa y no por la proporción áurea considerada ideal de belleza universal?
Al tener este resultado carácter local, se comenzó estudiando las proporciones de la figura humana en las artes locales cordobesas y se hallaron en el museo arqueológico local, esculturas y mosaicos con figuras humanas proporcionadas según la razón constante 1,3, más próxima al hombre de carne y hueso que al hombre ideal de Leonardo Da Vinci (Studio o El hombre de Vitrubio) o de LeCobusier (El Modulor).
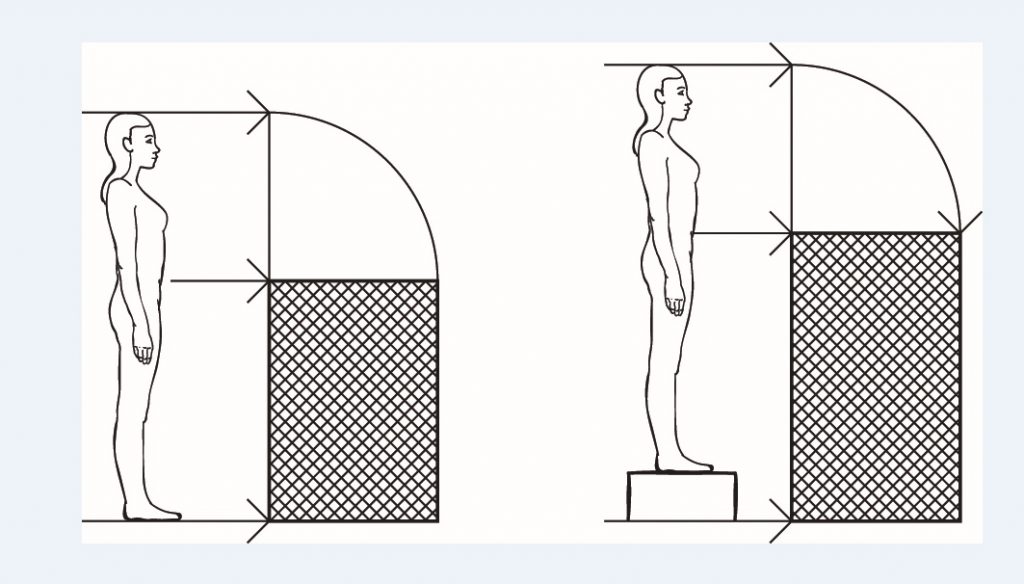 Proporción humana y proporción divina.
Proporción humana y proporción divina. Portada de la Mezquita de Córdoba.
Portada de la Mezquita de Córdoba.Se retomó el proyecto de analizar las proporciones de la arquitectura cordobesa y se hallaron múltiples ejemplos donde se utiliza esta proporción.
La portada y las arcadas de la Mezquita, la fachada interior de la Sinagoga, la portada de la casa de D. Juan Cosme de Paniagua, la iglesia de Santa Marina de las Aguas, la fachada del convento franciscano de Capuchinos…
A lo largo de los siglos, era evidente en Córdoba, la preferencia por esta proporción que el arquitecto Rafael de la Hoz bautizó como proporción cordobesa.
El siguiente paso fue establecer el origen geométrico de esta razón. Como la proporción áurea se obtiene como la razón entre el radio y el lado de un decágono regular, no fue complicado averiguar que la razón 1,3 correspondía a la proporción entre el radio y el lado de un octógono regular.
 Proporción áurea.
Proporción áurea. 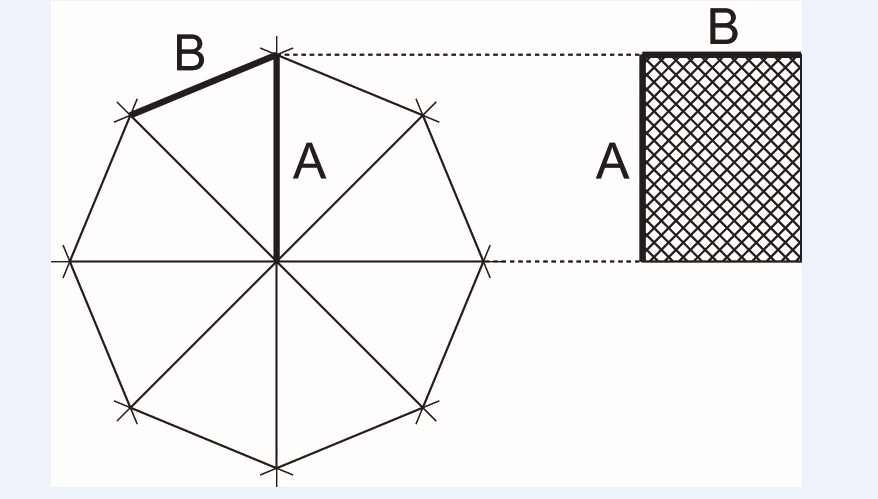 Proporción cordobesa.
Proporción cordobesa.
El octógono era una figura habitual en la arquitectura cordobesa: las cubiertas de la catedral, las bóvedas de la mezquita, los artesonados de Córdoba y Baena, la plaza de Aguilar, la planta de las torres de la Malmuerta, la fuente del Potro,…

Inicialmente se pensó que la proporción cordobesa tenía carácter local, pero fueron surgiendo estudios que identificaban esta proporción en distintos lugares y épocas. Algunos ejemplos son: las pirámides de Keops, Kefren y Mikerinos, en Egipto, el Panteón de Agripa y la basílica San Pablo Extramuros, en Roma, el arco del Triunfo y el hotel Mayenne, en París,…

En busca de simetría
- 4 junio, 2019
- Matemáticas para pensar
- 2 MIN
Un palíndromo es una palabra, una expresión o un número que se lee igual de izquierda a derecha, que de derecha a izquierda. En el caso de los números se utiliza también la expresión “números capicúas”. Contrariamente a lo que ocurre con las palabras o expresiones, es fácil obtener números palíndromos, de hecho, existen infinitos. Basta con tomar un número finito de cifras y repetirlas en sentido inverso, repitiendo, o no, el término del medio: 232, 3.773, 57.675, etcétera.
Tomemos un número cualquiera de dos dígitos, por ejemplo, el 23, que claramente no es igual a su simétrico, el número, 32, luego no es capicúa. ¿Qué ocurrirá si sumamos ambos, el número inicial y su simétrico? Veámoslo, 23 + 32 = 55. Obtenemos un número capicúa. ¿Ocurrirá esto con más números? Consideremos otro número, por ejemplo, el 57 y sumémosle su simétrico, 57 + 75 = 132, que, sin embargo, no es capicúa. Pero, probemos a realizar el mismo proceso de sumarle su simétrico al resultado anterior: 132 + 231 = 666, que resulta sí ser capicúa. Sigamos probando. El número 68, le sumamos su simétrico, 68 + 86 = 154, continuamos el proceso, 154 + 451 = 605, y un paso más, 605 + 506 = 1111, hasta que, de nuevo, obtenemos un número capicúa. Aunque esta vez hemos necesitado 3 pasos, o iteraciones. Podemos plantearnos, por lo tanto, el siguiente problema:
¿Si tomamos cualquier número natural y le sometemos al proceso iterativo de “sumar el simétrico del número”, se alcanzará siempre un número capicúa, es decir, tras un un número finito de pasos se obtendrá un palíndromo?
Empecemos viendo qué ocurre con los números de dos dígitos:
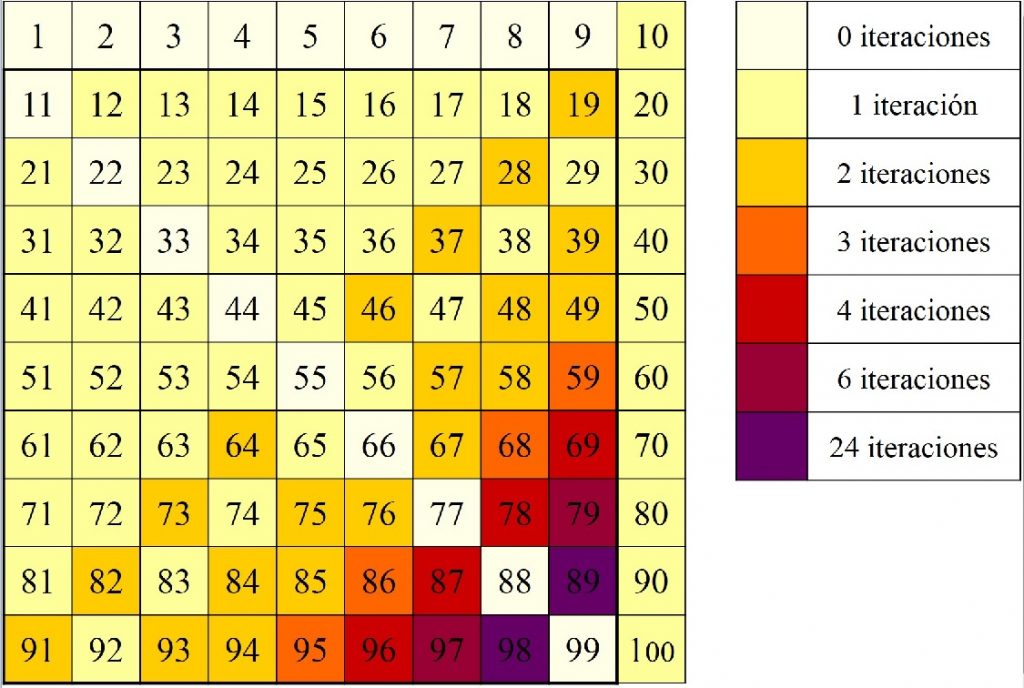
Para estos la respuesta es afirmativa, aunque para el 89, y su simétrico 98, se han necesitado 24 iteraciones para llegar al palíndromo. ¿Seguirá siendo cierta esta propiedad para números más grandes de tres o más dígitos? Lo cierto es que, a día de hoy, no se sabe la respuesta a esta pregunta. Este sigue siendo un problema matemático abierto. De hecho, el número 196, que no es muy grande, se desconoce si genera, mediante este proceso, un número capicúa.
La sucesión de los resultados de las 20 primeras iteraciones del número 196 es: 196, 887, 1.675, 7.436, 13.783, 52.514, 94.039, 187.088, 1.067.869, 10.755.470, 18.211.171, 35.322.452, 60.744.805, 111.589.511, 227.574.622, 454.050.344, 897.100.798, 1.794.102.596, 8.746.117.567, 16.403.234.045 y 70.446.464.506, que claramente no son palíndromos.
En la década de los años 80 se utilizaron los ordenadores para generar esta sucesión de números y averiguar si termina, o no, en un número capicúa. En 2011, Romain Dolbeau, con su programa “p196_mpi”, consiguió realizar un billón de iteraciones, con las cuales alcanzó un número de más de 400 millones de dígitos, sin conseguir el deseado capicúa. Y en 2015 alcanzó un número con un billón de dígitos, aún sin conseguir el objetivo de llegar a un palíndromo.
De hecho, el 196 no es el único número del que se desconoce si termina, con el proceso de “sumar el simétrico”, en un palíndromo. A la sucesión de números sospechosos de no generar un número capicúa se la conoce como sucesión de números Lychrel y es la sucesión A023108 en la Enciclopedia on-line de sucesiones de números enteros, de N. J. A. Sloane. Los primeros términos de esta sucesión son:
196, 295, 394, 493, 592, 689, 691, 788, 790, 879, 887, 978, 986, 1.495, 1.497, 1.585, 1.587, 1.675, 1.677, 1.765, 1.767, 1.855, 1.857, 1.945, 1.947, 1.997, …